Rumus Rangkaian Pembagi Arus dan Contoh Soal
Rangkaian pembagi arus (current divider circuits) adalah rangkaian yang memiliki dua atau lebih cabang paralel untuk mengalirkan arus, tetapi tegangannya sama untuk semua komponen dalam rangkaian paralel.
Jadi, arus dari sumber atau suplai akan terbagi menjadi sejumlah jalur paralel. Besar kecilnya arus yang mengalir tergantung dari besarnya hambatan di setiap jalur, semakin besar nilai hambatan maka arus yang mengalir semakin mengecil dan begitu pula sebaliknya.
Karakteristik utama dari rangkaian paralel adalah bahwa setiap jalur rangkaian dapat menghasilkan arus yang berbeda pada setiap cabang yang berbeda. Akan tetapi, tegangannya sama untuk semua jalur yang terhubung, yaitu VR1 = VR2 = VR3.... dst.
Oleh karena itu, tidak perlu lagi untuk menghitung masing-masing tegangan di setiap resistor. Artinya, cukup menghitung arus cabang saja berbekal dengan Hukum Arus Kirchhoff atau Kirchhoff’s Current Law (KCL) dan tentu saja Hukum Ohm.
Rumus Pembagi Arus Resistif
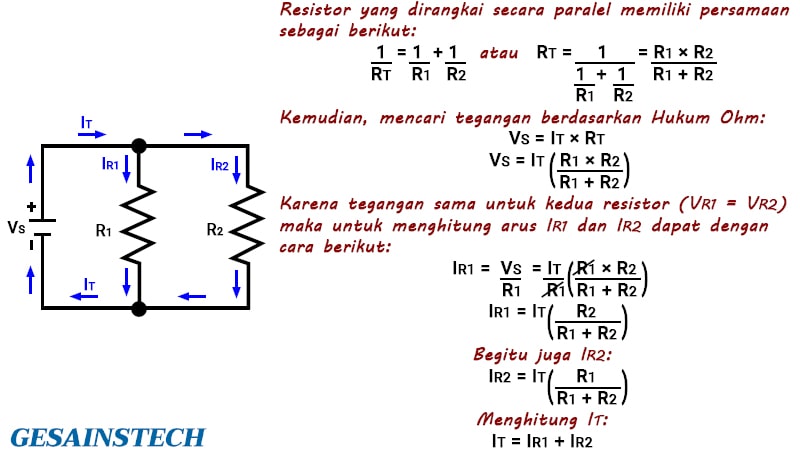
Bentuk paling dasar dan paling mudah dipahami dari jaringan pembagi arus pasif adalah dua resistor yang dirangkai bersama secara paralel.
Aturan pembagi arus memungkinkan kita untuk menghitung arus yang mengalir melalui setiap cabang resistif paralel sebagai persentase dari total arus.
Untuk lebih jelas lagi perhatikan rangkaian di bawah ini.
Pada rangkaian di atas pembagi arus dasar terdiri dari dua resistor, yaitu R1 dan R2 yang dirangkai secara paralel sehingga membagi suplai atau sumber arus (IS) menjadi dua arus terpisah IR1 dan IR2 sebelum akhirnya bergabung kembali dan arus kembali ke sumbernya.
Intinya adalah arus total sama dengan jumlah arus masing-masing cabang pada rangkaian paralel.
Kemudian, perhatikan bahwa persamaan di atas untuk setiap arus cabang memiliki resistor yang berlawanan dalam pembilangnya, yaitu untuk menyelesaikan I1 kita menggunakan R2 dan untuk menyelesaikan I2 kita menggunakan R1.
Ini karena setiap arus cabang berbanding terbalik dengan resistansinya sehingga resistansi yang lebih kecil memiliki arus yang lebih besar.
Rumus di atas dapat digunakan ketika dalam sebuah rangkaian paralel terdapat dua cabang hambatan.
Namun, apabila dalam sebuah rangkaian paralel terdapat lebih dari dua cabang hambatan maka untuk mencari besarnya arus per setiap cabang hambatan dapat menggunakan rumus di bawah.
Contoh Soal
Untuk lebih memahami lagi bagaimana mengenai pembagi arus, di bawah ini sudah diberikan beberapa contoh soal yang dapat Anda cermati.
Soal No.1
Dalam sebuah rangkaian, terdapat dua resistor yang dirangkai secara paralel. Nilai resistor pertama (R1) 4 Ohm, sedangkan resistor kedua (R2) 8 Ohm. Besarnya arus total (IT) atau arus sumber 6 Ampere. Tentukanlah besarnya arus yang mengalir pada IR1 dan IR2.
Soal No.2
Diketahui dua buah resistor dirangkai secara paralel. Apabila arus total atau arus sumbernya sebesar 6 mA, sedangkan R1 memiliki hambatan 2K Ω maka tentukanlah besarnya hambatan pada R2 jika IR2 adalah 2 mA.
Soal No.3
Dalam sebuah rangkaian terdapat tiga buah resistor yang dirangkai secara paralel, di mana R1 2 Ω, R2 3 Ω, dan R3 6 Ω. Selain itu, rangkaian paralel tersebut memiliki arus total atau arus sumber sebesar 2 A. Hitunglah besarnya arus yang mengalir pada IR1, IR2, dan IR3.
Soal No.4
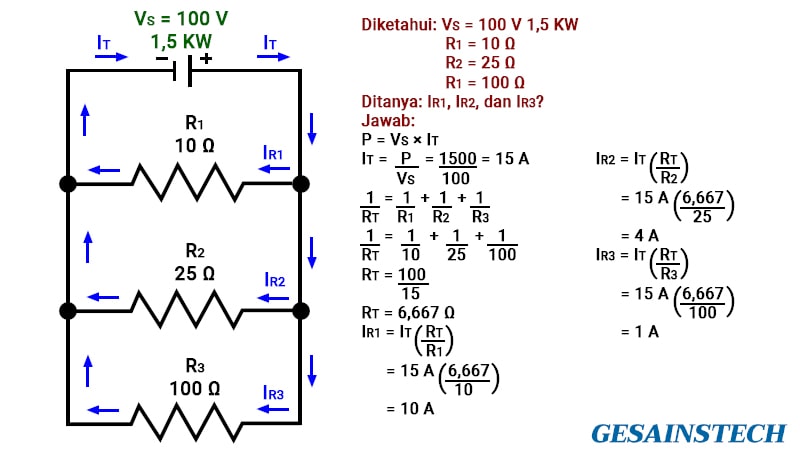
Dalam sebuah rangkaian terdapat tiga buah resistor yang dirangkai secara paralel, di mana R1 10 Ω, R2 25 Ω, dan R3 100 Ω. Selain itu, rangkaian paralel tersebut memiliki sumber tegangan (VS) sebesar 100 V 1,5 KW. Hitunglah besarnya arus yang mengalir pada IR1, IR2, dan IR3.
Ringkasan Pembagi Arus
Pembagi arus atau pembagian arus adalah proses menemukan arus cabang individu dalam rangkaian paralel di mana setiap elemen paralel memiliki tegangan yang sama.
Hukum arus Kirchhoff atau Kirchhoff’s current law (KCL) menyatakan bahwa jumlah arus individu yang memasuki persimpangan atau cabang akan sama dengan arus yang meninggalkannya.
Aturan pembagi arus Kirchhoff juga dapat digunakan untuk menemukan arus cabang individu ketika resistansi ekuivalen dan total arus rangkaian diketahui.
Ketika hanya dua cabang resistif yang terlibat, arus dalam satu cabang akan menjadi sebagian kecil dari total arus (IT). Jika dua cabang resistif paralel memiliki nilai yang sama, arus akan terbagi rata.
Dalam kasus tiga atau lebih cabang paralel, resistansi total (RT) yang setara digunakan untuk membagi arus total menjadi arus fraksional untuk setiap cabang yang menghasilkan rasio arus yang sama dengan kebalikan dari nilai resistifnya, sehingga nilai resistansi yang lebih kecil memiliki bagian terbesar dari arus.
Pasokan atau arus total (IT) menjadi jumlah dari semua arus cabang individu.